太さのある線 - you / WebGL

　とりあえず赤道を赤くしてみる

オブジェクト指向っぽくしてみる
クラスの書き方についてはプロトタイプによる継承にまとめたので、あまりツッコまんといてｗ
buildClassがクラスに設定している静的メソッドinitWithHookは既存オブジェクトのプロトタイプを置き換えて初期化を行う関数（「組み込み型と使う」参照）
グローバル関数buildHookClassは既存オブジェクトをcreateの第1引数として受け取り、そのプロトタイプに自分のプロトタイプを「上乗せ」するクラスを生成する
linkProgramで変なことをしているのは「C++言語と比べて」を参照
タッチイベントの設定もクラスにまとめてしまう
このクラスにはresizeイベントのフックも入っているが、イベントコールバックではthisがイベントが発生した要素になってしまうので、bindでthisを固定している
glTouchDrag.draw()は描画コールバック関数を自身のインスタンスを添えて呼び出す
- glTouchDragの外からコールバックを呼び出したいときに必要になる
- thisを渡しているが、this.cbDrawの形で呼び出しているため、本来はcbDrawの中ではthisは勝手にglTouchDragのインスタンスになっているはずである
- にもかかわらず律儀にthisを渡しているのは、コールバック関数にアロー関数を使いたかったから
視点は球中心から1.5離れたところ、ボールをちょっと離れたところから眺めた場合に相当
・・・にしても目立たない、太くしたい！
- 一応、GL（WebGL）にはlineWidthという関数があるが、仕様書に書かれている通り事実上機能していない
- 太さのある線を描きたければ自分でポリゴンをレンダリングする必要がある

3D空間で幅を持たせる

　赤道をリング状にしてみる

トライアングルストリップで書いている
共通部分はバンバン外部ファイルに移す
glProgramはVanillaGLProgramに、glContextはVanillaGLに、glTouchDragはVanillaGLTouchDragに改称
パースが付く（遠くの線が細く見える）
真横から見ると幅が0になる
一定の太さにしたい！

3D空間で棒状にする

　本当はトーラスにしたいが円を理想的にまあるく並べるのはできないので、角柱をカクカク曲げて輪にしてみる

五角柱を360回折り曲げて一周させている
奇数にしたのはグルグル回したときに太さの変化が少ないかなー、と思って
頂点の描画順
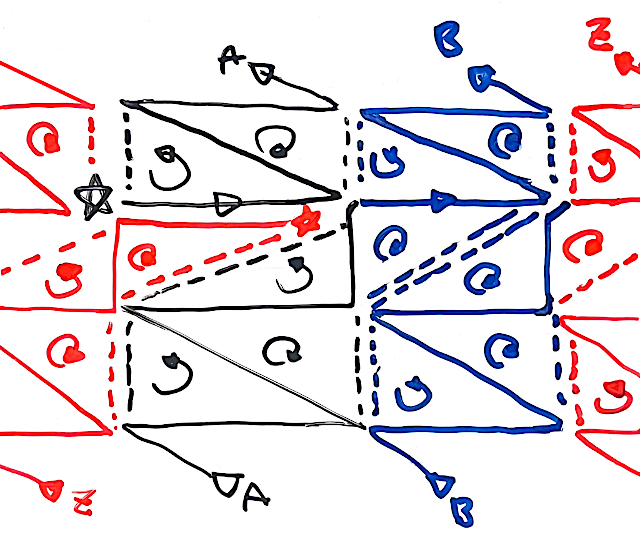
- 黒星がスタート地点で、赤星が終了地点
- 横方向がトーラスの円周方向、縦方向は断面多角形の辺方向
- 最初と最後の2点のみ重複
- この順序でトライアングルストリップを描かせると一発でトーラス全体が描ける
- 丸い矢印は、矢印の方向に頂点が回っていれば表
表裏も問題ないはずなので、カリングすれば描画量が半分になる
- 今は深度テストをしていないので全部のポリゴンが描画の対象になっており、実際に全部のポリゴンが半透明の状態で見えている
- 深度テストをしなくても、表面がこっちを向いているポリゴンだけ描画すれば描画量が半分になる（カリング）
- gl.enable・gl.disableにgl.CULL_FACEを渡すことで切り替えられる
頂点列の生成: まず、基準となる五角形ポリゴンを中心(1, 0, 0)、XZ平面上に生成する
これを原点を中心にZ軸を軸として回転しながら使う
始点側ポリゴンと終点側ポリゴンを結ぶ頂点列を作っていく
- 初期状態では始点側が基準ポリゴン、終点側がそれを1/360回転させたもの
- この回転計算のためにMat4に行列とベクトルの積を計算する関数mulを実装している（後述）
- 次回以降は始点側ポリゴンは前回の終点側ポリゴン、終点側ポリゴンは新たに計算する
- 最終回では誤差を防ぐため、終点側ポリゴンは基準ポリゴンを使い回す
- 最後に先頭から2個だけ頂点をコピーして終了、黒星と赤星の頂点に相当する
Mat4をクラス化
- Arrayを継承しているのでArrayの機能は全部使える
- createは引数なしなら単位行列を生成、引数の数が1で引数が配列だった場合はそのコピーで初期化、そうでなければArrayコンストラクタに引数をそのまま渡して生成された配列を使う
- インスタンスプロパティとしてrows・colsを定義
- initは要素数を強制的に16にし、初期化されていない要素には0を設定する
- mulはインスタンスメソッドになっており、引数で指定された配列をベクトルとみなし、thisが示す行列と引数で指定されたベクトルの積を求め、新しい配列として返す
- mulが呼んでいるcolumnは引数で指定された列を新しい配列として返す
- カラムメジャーなので列はArray.sliceすればよいが、行はそうはいかないのでrowは実装していない
ぐるっと回っているため、軸キューブと前後関係を解決することができていない
- いや前から球面座標グリッドと軸キューブの関係は破綻していたのだが、球面座標グリッドが細くて気が付かなかっただけ
- どちらかを不透明にして深度テストを使えば解決するが・・・
パースが付くが、奥行き感を捉えやすいのでこれはこれでアリと思う
もうちょっと楽に書けないのん？

2D空間で一定の幅にする

　赤道だけパースを無視して計算すれば一定の太さになるんじゃなかろうか？

と言いつついきなりパースがついているが、それは最後の方で解説
各セグメントの線分をスクリーン座標に変換してから、線の太さの半分だけ平行に離れた直線を引いて、同様に引いた隣のセグメントとの交点を求めていけばよい（下図の\(V\)）
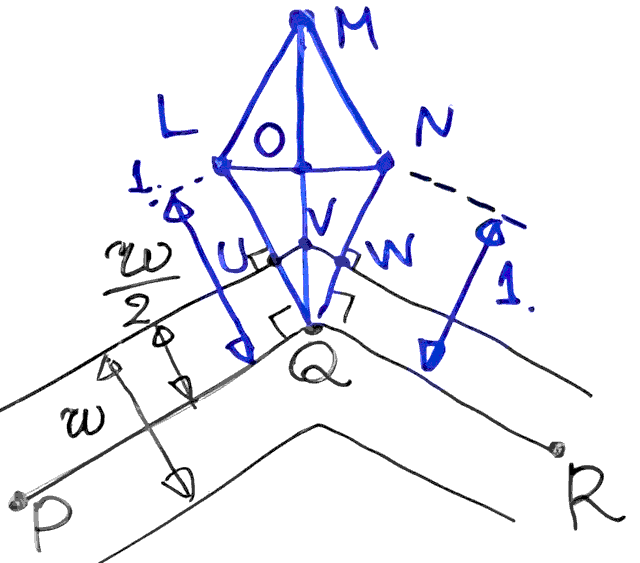
点\(P\)・\(Q\)・\(R\)が各線分の中心であり、頂点列でこの順に指定する
- \(w\)を描画する直線の太さとして、点\(Q\)から線分\(PQ\)に垂直に、反時計回りの方向へ距離\(w/2\)の点を\(U\)、距離1の点を\(L\)とする
- 点\(Q\)から線分\(QR\)に垂直に、反時計回りの方向へ距離\(w/2\)の点を\(W\)、距離1の点を\(N\)とする
- 点\(U\)を通り線分\(QL\)に垂直な直線と、点\(W\)を通り線分\(QN\)に垂直な直線の交点を\(V\)とする
  - この点の座標を求めたい
- 三角形\(QVU\)と\(QVW\)を比べると、頂点\(U\)・\(W\)は直角で、辺\(QU\)・\(QW\)は長さ\(w/2\)で、辺\(QV\)が共通になっているから、直角三角形の合同条件からこのふたつの三角形は合同で、角\(VQU=VQW\)である
- 一方、線分\(LN\)と半直線\(QV\)が交わる点を\(O\)とすると、三角形\(QLO\)と\(QNO\)は角\(OQL=VQU\)、角\(OQN=VQW\)よりこのふたつの角は等しく、辺\(QL=QN\)は長さ1で等しく、辺\(QO\)は共通なので合同である
- よって角\(QOL=QON\)であり、\(LN\)は線分なのだから\(LON\)は180度であり、このふたつの角は直角である
- 今まで出てきた三角形4つは全て直角三角形であり、角\(VQU=VQW=LQO=NQO\)なので相似になっている
- ここでベクトルの力を借り、ベクトル\(QL\)と\(QN\)の和をベクトル\(QM\)とする
- 詳細は省略するがベクトルの和の性質から四角形QLMNは辺の長さが1のひし形になっているので、この四角形の中にできている三角形は全て合同で、線分QOの長さはベクトル\(QM\)の長さの半分である
- これで\(QL\)・\(QO\)・\(QU\)の長さが既知となったので相似比から\(QV\)の長さが分かる
  \begin{align*} QV&=\frac{w}{2}\cdot\frac{1}{QM/2}=\frac{w}{2}\cdot\frac{2}{QM} \eol &=\frac{w}{QM} \end{align*}
- 方向はベクトル\(QM\)の方向になる
- 実際に計算する際には横倒しのまま\(QM'\)を計算して、それを反時計回りに90度回せばよい
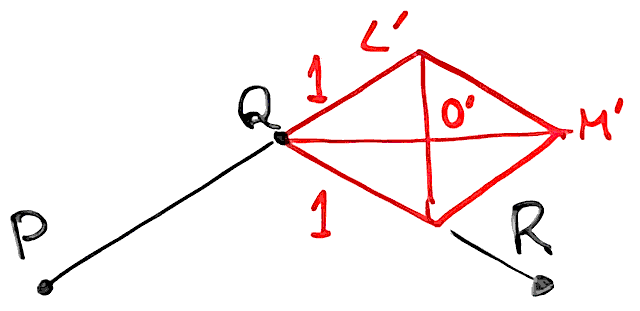
手順をまとめると以下のようになる
- ベクトル\(PQ\)・\(QR\)を長さ1に正規化して足し、\(QM'\)を求める
- \(QM'\)を90度回転させ、\(QM\)とする
- 点\(Q\)から\(QM\)の方向へ、\(w/|QM|\)だけ離れた位置が求める頂点である
- \(QM\)は正規化する必要があるため、最終的に\(|QM|^2\)で割ることに注意
頂点を与える順を逆にすると、反対側に\(V\)ができる（各自で確認されたし）
実装したのが頂点シェーダーthickline.vs
頂点シェーダーは頂点列の入力ひと組に対し、頂点列をひと組出力し、これがトライアングルストリップの各頂点になる
各頂点に対して点\(V\)を計算して出力することになるが、各入力頂点データに計算に必要なすべてのデータを含めなければならない
つまり、頂点をひとつ計算するために\(P\)・\(Q\)・\(R\)の情報が必要になる
さらにトライアングルストリップで線を描画するためには各線分について三角形がふたつ必要になる
もうひとつの頂点は反対側に\(w/2\)だけ離れた点で、これは頂点の与え方を逆にすればよい
結局、線分ひとつにつき、\((P, Q, R)\)という頂点の組と、\((R, Q, P)\)という頂点の組を与える必要がある

頂点の指定順はこうなる

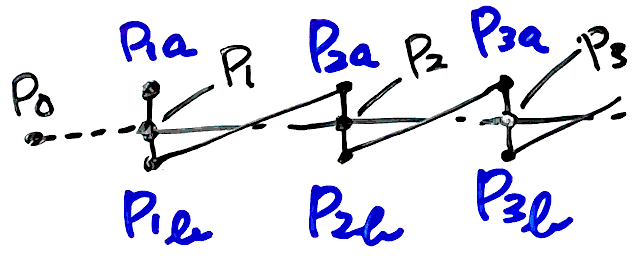
VS出力頂点	入力頂点と順序
\(P_{1a}\)	\(P_0, P_1, P_2\)
\(P_{1b}\)	\(P_2, P_1, P_0\)
\(P_{2a}\)	\(P_1, P_2, P_3\)
\(P_{2b}\)	\(P_3, P_2, P_1\)
\(P_{3a}\)	\(P_2, P_3, P_4\)
\(P_{3b}\)	\(P_4, P_3, P_2\)

赤道の場合は閉曲線なのでどの点についても前の点が存在するが、端のある線を書く場合は始点の前の点を生成して指定する必要がある（\(P_1-(P_2-P_1)=2P_1-P_2\)を指定しておけばいいだろう）
終点についても同様に、最後の点の次の点を指定する必要がある
赤道は同一平面（XY平面）に収まっているので、入力頂点はデータ量削減のため\(x\)と\(y\)だけ指定している
最初に各点の射影座標を求めたら.wで割って2Dの座標に直す
さらにスクリーンの大きさが(-1, +1)の範囲に対応しているので、アスペクト比をかけて表示上の正方形が数値上でも正方形になるようにしておく
出力頂点の位置を求めたら、逆にアスペクト比で割って射影座標系に戻しておく、Zは0、Wは1でよい
uThicknessは.xyがアスペクト比指定で、キャンバスの幅と高さを指定する
.zが線の太さでGLキャンバスのピクセルの半分が単位になっており、キャンバス高さの0.5%にしている
2D空間に投影したあとの線分の角度がキツくなると、頂点\(V\)がとんでもなく遠くになってしまうことがある
- 角\(PQR=0\)のときに無限遠
- シェーダーコードの最後の方に出てくるlength(n)が\(QM\)の長さを示すが、角度をキツくしていくと\(QM\)の長さはどんどん0に近づき（シェーダー中のベクトルnがどんどん短くなり）、\(QV\)の長さが際限なく大きくなるため、適当に制限をつける必要がある
- 例えば角\(PQR\)が90度よりもキツくなったら制限をかける
- 角\(PQR\)が90度のとき、四角形\(QLMN\)は辺の長さが1の正方形になるので、対角線になる\(QM\)の長さは\(\sqrt 2\)である
- dはその逆数なので、最大値を\(1/\sqrt 2\neareq 0.707\)に抑え込む
- min関数がそれ（maxではなくminなので注意、恥ずかしいが実はハマった）
- 試しにminなしで実行してみるとよい（コメントアウトしてある文）
対策しても赤道を水平にして水平方向に回転させると端の方がチラチラするが、これがこの方式の欠点というか限界というか
このままだとパースはつかないが、この例ではパースをつけている
- p2を射影変換した直後にp2.wを変数wに保持しておき、gl_Positionを求めるときに線分のオフセット量をこのwで割る
- 変数wに関する演算を取り除くとパースがつかなくなる
見た目は「3D空間で棒状にする」とだいたい同じになり、頂点量はぐっと少なくなる
頂点シェーダーの演算量は増える

途中で太さを変えたい

　とりあえず計算だけ

「2D空間で一定の幅にする」の図で\(QU\)と\(QW\)の長さが違う場合に相当
線分\(PQ\)からその太さの半分だけ離れた線分（半直線\(VU\)のUより遠い部分）を位置ベクトル\(\bvec p\)で、線分\(QR\)については\(\bvec q\)で表すことにする
各ベクトルの始点・終点をそれぞれ位置ベクトル\(\bvec p_0\)・\(\bvec p_1\)・\(\bvec q_0\)・\(\bvec q_1\)とする
点Uが\(\bvec p_1\)に、点\(W\)が\(\bvec q_0\)に相当する
目標はふたつの線分の交点を求めることである
ベクトル\(p\)・\(q\)は媒介変数\(s\)・\(t\)を用いて以下のように表現できる
\begin{align*} \bvec{p} &= \bvec{p_0} + s (\bvec{p_1} - \bvec{p_0}) \eol \bvec{q} &= \bvec{q_0} + t (\bvec{q_1} - \bvec{q_0}) \end{align*}
このふたつが等しくなる点を求めたいので、以下のように計算する
\begin{align*} \bvec{p_0} + s (\bvec{p_1} - \bvec{p_0}) &= \bvec{q_0} + t (\bvec{q_1} - \bvec{q_0}) \eol s (\bvec{p_1} - \bvec{p_0}) - t (\bvec{q_1} - \bvec{q_0}) &= \bvec{q_0} - \bvec{p_0} \end{align*}
連立方程式を解くのが面倒くさいので、行列の知識を借りる
\begin{align*} \begin{pmatrix} \bvec{p_1} - \bvec{p_0} & -(\bvec{q_1} - \bvec{q_0}) \end{pmatrix} \begin{pmatrix}s \\ t\end{pmatrix} &= \bvec{q_0} - \bvec{p_0} \end{align*}
ここで\(\bvec p_0=(x_{p0},\ y_{p0})\)のように置き、\(\bvec {p_1} - \bvec {p_0} = (dx_p,\ dy_p)\)、\(\bvec {q_1} - \bvec {q_0} = (dx_q,\ dy_q)\)と置く
\begin{align*} \begin{pmatrix} dx_p & -dx_q \\ dy_p & -dy_q \end{pmatrix} \begin{pmatrix} s \\ t \end{pmatrix} &= \begin{pmatrix} x_{q0} - x_{p0} \\ y_{q0} - y_{p0} \end{pmatrix} \eol \begin{pmatrix}s \\ t\end{pmatrix} &= \begin{pmatrix} dx_p & -dx_q \\ dy_p & -dy_q \end{pmatrix}^{-1} \begin{pmatrix} x_{q0} - x_{p0} \\ y_{q0} - y_{p0} \end{pmatrix} \eol &= \frac{1}{ dx_q dy_p - dx_p dy_q } \begin{pmatrix} -dy_q & dx_q \\ -dy_p & dx_p \end{pmatrix} \begin{pmatrix} x_{q0} - x_{p0} \\ y_{q0} - y_{p0} \end{pmatrix} \end{align*}
\(s\)か\(t\)だけ求めればよいので、
\begin{align*} s &= \frac{ dx_q (y_{q0} - y_{p0}) -dy_q (x_{q0} - x_{p0}) }{ dx_q dy_p - dx_p dy_q } \end{align*}
とすれば、\(\bvec{p} = \bvec{p_0} + s (\bvec{p_1} - \bvec{p_0})\)が求める点である
正直、計算したくない
頂点データに\(P\)・\(Q\)・\(R\)の他に\(PQ\)の太さと\(QR\)の太さも載せる必要がある
\(P\)・\(Q\)・\(R\)が直線上に並ぶと交点を計算できなくなり破綻するので注意
- まっすぐ線が伸びている場合と、先ほども問題になった折り返す場合が含まれる
- 始点の前・終点の向こうの頂点を直線上に置けないので、幅0の垂直線とかを使えばいいのかな

17 Jul 2024	カリングに言及
15 Jul 2024	初稿